Unit Circle: A Key to Trigonometric Functions

Introduction

The unit circle stands as a foundational concept in mathematics, particularly within the realm of trigonometry. It serves as a powerful bridge connecting geometry and algebra, offering a visual and intuitive framework for understanding complex mathematical relationships. This exploration will take you on a journey through the intricacies of the unit circle, starting with its basic definition and progressing to its advanced applications in various fields. Prepare to unlock a deeper understanding of trigonometry through this elegant and essential tool.

Defining the Cornerstone: What is the Unit Circle?

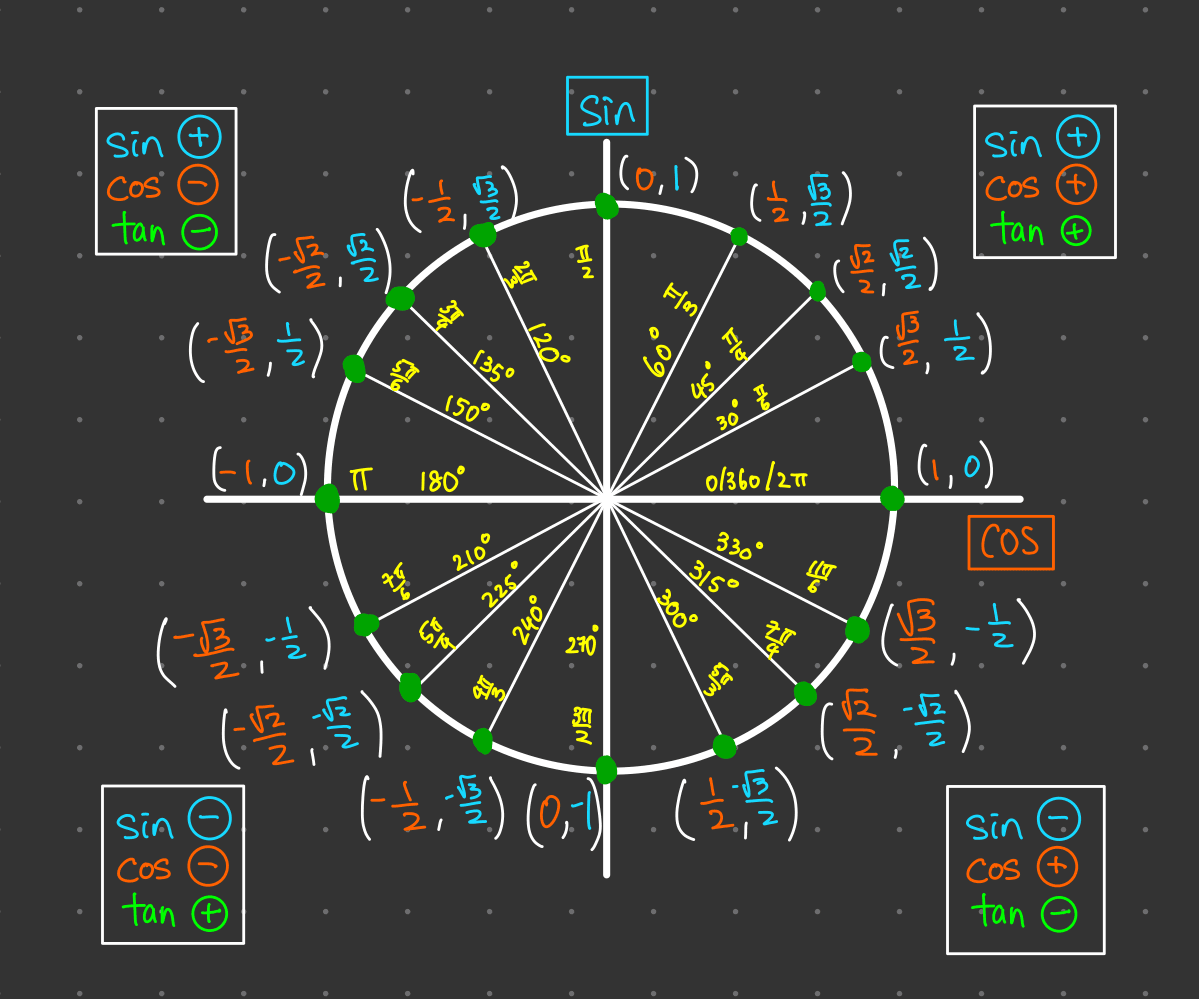
At its core, the unit circle is defined as a circle with a radius of exactly one unit, centered at the origin (0,0) of the Cartesian coordinate system in the Euclidean plane . The term "unit" signifies that the radius has a length of 1, and this unit can represent any standard measure of length, such as meters, inches, or any other appropriate unit. In trigonometry, the unit circle is most frequently positioned with its center at the origin of a coordinate plane, making it an invaluable tool for visualizing angles and trigonometric functions . From a topological perspective, the unit circle is also recognized as S¹, representing a one-dimensional unit n-sphere . Algebraically, the unit circle is represented by a simple yet fundamental equation, x² + y² = 1. This equation is derived directly from the Pythagorean theorem, where for any point (x, y) on the circle, the sum of the squares of its coordinates equals the square of the radius (1² = 1). Some educational contexts even refer to it as a "trigonometric circle," emphasizing its central role in defining and visualizing trigonometric functions.

The mathematical significance of the unit circle is profound, especially in the study of trigonometry . It provides a visual and intuitive approach to understanding angles and trigonometric functions that extends beyond the traditional right-triangle definitions . For instance, the unit circle allows for the definition of trigonometric functions for angles of any magnitude, not just those between 0 and 90 degrees that form a right triangle . The definitions of sine and cosine on the unit circle are particularly elegant: for an angle θ, cos θ corresponds to the x-coordinate and sin θ corresponds to the y-coordinate of the point where the terminal side of the angle intersects the circle . This is a more concise and versatile definition compared to the ratios of sides in a right triangle (adjacent/hypotenuse and opposite/hypotenuse, respectively) . Furthermore, the unit circle serves as a powerful tool for understanding trigonometric functions across all four quadrants of the coordinate plane and for visualizing their periodic nature . It simplifies the process of solving angular sines, cosines, and tangents, making it a central concept in trigonometry . The consistent definition of the unit circle across various mathematical resources underscores its fundamental importance. The algebraic representation, x² + y² = 1, acts as a constraint that every point on the unit circle must satisfy, directly linking the geometric concept of a circle with its algebraic description. This unification of geometry and algebra is a cornerstone of the unit circle's mathematical significance.

Key Properties: The Anatomy of a Unit Circle

The unit circle possesses several key properties that make it such a valuable tool in mathematics. First and foremost, its radius is always 1 unit, and its center is invariably located at the origin (0,0) of the Cartesian plane . This standardization simplifies many calculations and relationships within trigonometry.

A crucial property of the unit circle is how it relates angles to coordinates. For any angle θ, measured counterclockwise from the positive x-axis, the coordinates of the point where the terminal side of the angle intersects the unit circle are given by (cos θ, sin θ) . This fundamental relationship is consistently highlighted across numerous resources. The x-coordinate of this point directly corresponds to the cosine of the angle, while the y-coordinate corresponds to the sine of the angle .

Determining the coordinates for any given angle on the unit circle involves understanding the connection between angles, special right triangles, and the circle's symmetry . For common angles like 30°, 45°, and 60° (or their radian equivalents), the coordinates can be derived using the properties of 30-60-90 and 45-45-90 triangles inscribed within the unit circle . The symmetry of the unit circle across the x-axis, y-axis, and the origin allows for the determination of coordinates in the second, third, and fourth quadrants based on the values in the first quadrant, with appropriate adjustments to the signs of the x and y coordinates . For instance, the values of cosine and sine repeat across the four quadrants, but their signs depend on the quadrant . Reference angles, which are the acute angles formed by the terminal side of an angle and the x-axis, are crucial for finding these coordinates in different quadrants.

To illustrate these key properties, consider the following table of common angles and their corresponding coordinates on the unit circle:

Key Table 1: Common Angles and Their Coordinates

The fact that the coordinates of any point on the unit circle directly correspond to the cosine and sine of the angle establishes a fundamental connection between geometry and trigonometric functions. Understanding how to derive these coordinates using special triangles and the inherent symmetry of the circle is therefore essential for effectively utilizing the unit circle.

The Unit Circle and Trigonometric Functions: A Symbiotic Relationship

The unit circle provides an elegant and intuitive way to define the fundamental trigonometric functions: sine, cosine, and tangent. As established, for any angle θ, the sine (sin θ) is defined as the y-coordinate of the point where the terminal side of the angle intersects the unit circle . Similarly, the cosine (cos θ) is defined as the x-coordinate of that same point . The tangent (tan θ) of the angle is then defined as the ratio of the sine to the cosine, or y/x . Geometrically, the tangent can also be visualized as the slope of the line segment connecting the origin to the point (cos θ, sin θ) on the unit circle . In some contexts, the tangent is also described as the slope of the tangent line to the unit circle at the point (1,0), extended to intersect the line containing the terminal side of the angle .

The unit circle transforms these abstract trigonometric ratios into tangible geometric entities. The sine of an angle becomes the vertical distance of the point on the circle from the x-axis, while the cosine becomes the horizontal distance from the y-axis . The tangent represents the steepness of the line connecting the origin to that point.

Beyond these primary trigonometric functions, the unit circle also helps define the other three: cotangent (cot θ), secant (sec θ), and cosecant (csc θ). The cotangent is the reciprocal of the tangent, defined as cos θ / sin θ or x/y . The secant is the reciprocal of the cosine, defined as 1 / cos θ or 1/x . Finally, the cosecant is the reciprocal of the sine, defined as 1 / sin θ or 1/y . These reciprocal functions also have geometric interpretations on the unit circle, although they are less direct than those of sine, cosine, and tangent. For instance, the secant is related to the length of a line segment from the origin along the x-axis to the point where the tangent line at (1,0) intersects the line containing the terminal side of the angle.

The unit circle provides a cohesive framework for understanding all six trigonometric functions through the simple geometric interpretations of coordinates and their ratios. This visual representation significantly simplifies the relationships between these functions, making them more accessible and easier to remember.

Solving Trigonometric Equations with the Unit Circle: A Visual Approach

The unit circle offers a visual and intuitive method for solving trigonometric equations. The process generally involves the following steps:

First, isolate the trigonometric function in the given equation . For example, if you have an equation like 2 sin θ - 1 = 0, you would isolate sin θ to get sin θ = 1/2.

Next, identify the angles on the unit circle where the trigonometric function has the desired value . Remember that sin θ corresponds to the y-coordinate, cos θ to the x-coordinate, and tan θ to the ratio y/x. For sin θ = 1/2, you would look for points on the unit circle where the y-coordinate is 1/2.

Finally, consider all possible solutions within the specified range or find the general solutions. Since trigonometric functions are periodic, there can be infinitely many solutions. For solutions within a specific interval (e.g., 0 ≤ θ < 2π), you identify all the angles within that range that satisfy the equation. For general solutions, you add multiples of the period to these initial solutions (2πk for sine and cosine, πk for tangent, where k is an integer) .

Let's look at some practical examples:

Example 1: Solve sin θ = 1/2 for 0 ≤ θ < 2π . On the unit circle, the y-coordinate is 1/2 at two points in the interval. The x-coordinate on the unit circle is -√3/2 at two points. These occur at θ = 5π/6 (150°) in the second quadrant and θ = 7π/6 (210°) in the third quadrant. A vertical line at x = -√3/2 intersecting the unit circle illustrates these solutions.

Example 3: Solve tan θ = 1 for 0 ≤ θ < 2π . Tangent is the ratio of y/x. tan θ = 1 when the y and x coordinates are equal (and non-zero). This happens at θ = π/4 (45°) in the first quadrant and θ = 5π/4 (225°) in the third quadrant. These points lie on the lines y = x and y = x extended through the origin.

For equations involving cosecant, secant, or cotangent, you can first convert them to their reciprocal functions (sine, cosine, or tangent, respectively) and then use the same method . For instance, solving csc x = 2 is equivalent to solving sin x = 1/2.

The unit circle transforms the algebraic task of solving trigonometric equations into a geometric visualization of finding points on the circle that meet specific coordinate or slope conditions. This visual approach can make the process more intuitive and easier to understand compared to purely algebraic manipulations.

Visualizing Periodicity: The Rhythmic Nature of Trigonometric Functions

One of the remarkable aspects of trigonometric functions is their periodic nature, meaning their values repeat at regular intervals. The unit circle provides a clear visual representation of this phenomenon . As an angle θ increases beyond 2π radians (or 360°), the point (cos θ, sin θ) on the unit circle simply retraces its path. This means that after one full rotation, the coordinates, and therefore the sine and cosine values, repeat .

The period of a trigonometric function is the smallest positive value k for which f(x + k) = f(x) for every x . For both the sine and cosine functions, the period is 2π . This is because one complete rotation around the unit circle corresponds to an angle of 2π radians (or 360 degrees), and after this rotation, you return to the same point, implying the values of sine (y-coordinate) and cosine (x-coordinate) are the same as they were at the starting angle.

Consider a point moving counterclockwise around the unit circle. As the angle increases from 0 to 2π, the y-coordinate (sine value) starts at 0, increases to 1 at π/2, decreases to 0 at π, reaches -1 at 3π/2, and returns to 0 at 2π. If the angle continues to increase beyond 2π, this pattern repeats. Similarly, the x-coordinate (cosine value) starts at 1, decreases to 0 at π/2, reaches -1 at π, increases to 0 at 3π/2, and returns to 1 at 2π, again repeating for angles greater than 2π.

This cyclical movement on the unit circle directly corresponds to the wave-like graphs of the sine and cosine functions. Imagine "unrolling" the circumference of the unit circle onto a horizontal axis representing the angle θ. The height of the sine wave at each point θ corresponds to the y-coordinate of the point on the unit circle at that angle, and similarly, the height of the cosine wave corresponds to the x-coordinate . The completion of one full circle (2π radians) on the unit circle corresponds to one complete cycle of the sine and cosine waves.

Radians vs. Degrees: Two Ways to Measure Angles

Angles can be measured using different units, with degrees and radians being the most common. The unit circle provides a natural framework for understanding radians. A radian is defined as the angle subtended at the center of a circle by an arc whose length is equal to the radius of the circle . Since the unit circle has a radius of 1 unit, an arc length of 1 unit on the unit circle corresponds to a central angle of 1 radian . A full circle has a circumference of 2πr, which for a unit circle (r=1) is 2π. Therefore, a full rotation around the unit circle corresponds to an angle of 2π radians.

Degrees, on the other hand, divide a full circle into 360 equal parts . One degree is thus 1/360th of a full rotation.

It is often necessary to convert between these two units. The fundamental relationship is that 2π radians is equivalent to 360 degrees, which simplifies to π radians = 180 degrees . From this, we can derive the conversion formulas:

• To convert from degrees to radians: radians = degrees × π/180 .
• To convert from radians to degrees: degrees = radians × 180/π .

Let's look at some examples:

• Convert 60 degrees to radians: 60 × π/180 = π/3 radians.
• Convert π/4 radians to degrees: (π/4) × 180/π = 45 degrees.

The unit circle is often marked with angles in both degrees and radians, providing a visual reference for these conversions.

Key Table 2: Common Angles in Degrees and Radians

While degrees are commonly used in everyday contexts, radians are often preferred in higher mathematics, especially in calculus and physics, because they simplify many formulas and relationships related to circles and rotational motion . The direct relationship between radians and arc length on the unit circle makes them a more natural unit for many mathematical applications.

Practical Examples and Diagrams: Making it Accessible

To truly grasp the power of the unit circle, it is essential to visualize its components and work through practical examples. Throughout this explanation, the importance of clear and labeled diagrams has been implicit. A standard unit circle diagram typically shows angles in both degrees and radians at key points around the circle, along with the corresponding (cosine, sine) coordinates. These diagrams serve as a visual aid for understanding the relationships between angles and trigonometric values.

Furthermore, the step-by-step examples provided in the section on solving trigonometric equations illustrate how to apply the principles of the unit circle to find solutions. For instance, when solving sin θ = 1/2, visualizing the unit circle and identifying the angles where the y-coordinate is 1/2 provides a clear path to the solutions. Similarly, for other trigonometric functions, the unit circle acts as a visual map to locate the angles that satisfy the given conditions.

Real-World Applications: The Unit Circle in Action

The unit circle is not merely an abstract mathematical concept; it has numerous practical applications in various scientific and engineering fields .

In physics, the unit circle and trigonometric functions derived from it are fundamental for modeling wave motion, such as sound waves and light waves . They are also used to describe oscillations, like the motion of a pendulum or a spring . Furthermore, the unit circle is crucial in analyzing circular motion, including planetary orbits and the rotation of objects .

Engineering relies heavily on the principles of the unit circle for analyzing systems involving rotation, such as gears, motors, and turbines . In signal processing, techniques like Fourier analysis, which are vital for sending and receiving signals, are entirely based on trigonometric functions derived from the unit circle . Electrical engineering also utilizes these concepts, particularly in the analysis of alternating current (AC) circuits.

In computer graphics, the unit circle plays a key role in implementing rotations and other transformations (like scaling and skewing) of objects in both 2D and 3D graphics . These transformations are essential for creating realistic and dynamic visual experiences.

Even in navigation and GPS (Global Positioning System) technologies, the principles of the unit circle underpin the accurate calculations of distances, bearings, and angles necessary for geolocation and map-based systems .

Through its connection to trigonometric functions, the unit circle provides a fundamental mathematical tool for modeling and analyzing a vast array of real-world phenomena involving periodic or circular motion. Its widespread applications across diverse disciplines underscore its practical significance far beyond the realm of theoretical mathematics.

Conclusion: The Enduring Significance of the Unit Circle

In summary, the unit circle is a circle with a radius of one unit, centered at the origin of the Cartesian plane. Its key properties include its radius and center, as well as the fundamental relationship between angles and the coordinates of points on the circle, given by (cos θ, sin θ). The unit circle provides a visual and intuitive way to define all six trigonometric functions, making their relationships and behaviors across different quadrants easily understandable. It serves as a powerful tool for solving trigonometric equations by transforming them into geometric problems on the circle. Furthermore, the unit circle elegantly illustrates the periodic nature of trigonometric functions, particularly sine and cosine, and provides a natural way to understand radian measure in relation to degrees. Its applications are far-reaching, spanning physics, engineering, computer graphics, and navigation, demonstrating its practical importance in modeling and analyzing real-world phenomena. The unit circle remains an enduring and significant concept in mathematics, providing a foundational understanding for more advanced topics in trigonometry and beyond.

Works cited

1. en.wikipedia.org, accessed March 25, 2025, https://en.wikipedia.org/wiki/Unit_circle#:~:text=In%20mathematics%2C%20a%20unit%20circle,system%20in%20the%20Euclidean%20plane.
2. Introduction to the unit circle | Mathematics Curriculum Companion - Arc, accessed March 25, 2025, https://arc.educationapps.vic.gov.au/learning/sites/mcc/VCMMG368
3. Unit circle - Wikipedia, accessed March 25, 2025, https://en.wikipedia.org/wiki/Unit_circle
4. Equation of a Unit Circle - Cuemath, accessed March 25, 2025, https://www.cuemath.com/geometry/unit-circle/
5. UNIT CIRCLE Definition & Meaning - Merriam-Webster, accessed March 25, 2025, https://www.merriam-webster.com/dictionary/unit%20circle
6. What is a unit circle? - Tutorax, accessed March 25, 2025, https://tutorax.com/blogue/en/what-is-a-unit-circle/
7. www.cuemath.com, accessed March 25, 2025, https://www.cuemath.com/geometry/unit-circle/#:~:text=The%20equation%20of%20a%20unit%20circle%20is%20x2%20%2B%20y,help%20of%20the%20distance%20formula.
8. Unit of a Circle: A Comprehensive Guide - Livius Prep, accessed March 25, 2025, https://www.liviusprep.com/a-comprehensive-guide-to-the-unit-circle.html
9. APC The Unit Circle - Active Calculus, accessed March 25, 2025, https://activecalculus.org/prelude/sec-circular-unit-circle.html
10. What is Unit Circle? Definition, Chart, Equation, Examples, Facts - SplashLearn, accessed March 25, 2025, https://www.splashlearn.com/math-vocabulary/unit-circle
11. Unit Circle - Math is Fun, accessed March 25, 2025, https://www.mathsisfun.com/geometry/unit-circle.html
12. science.howstuffworks.com, accessed March 25, 2025, https://science.howstuffworks.com/math-concepts/unit-circle.htm#:~:text=A%20unit%20circle%20defines%20right,triangles%20relate%20to%20one%20another.
13. Trig unit circle review (article) - Khan Academy, accessed March 25, 2025, https://www.khanacademy.org/math/algebra2/x2ec2f6f830c9fb89:trig/x2ec2f6f830c9fb89:unit-circle/a/trig-unit-circle-review
14. How to Use the Unit Circle in Trigonometry - Science | HowStuffWorks, accessed March 25, 2025, https://science.howstuffworks.com/math-concepts/unit-circle.htm
15. Why is the Unit Circle so important? : r/trigonometry - Reddit, accessed March 25, 2025, https://www.reddit.com/r/trigonometry/comments/ibdy0u/why_is_the_unit_circle_so_important/
16. [High School Trigonometry] What is the significance of the unit circle to trigonometry? : r/learnmath - Reddit, accessed March 25, 2025, https://www.reddit.com/r/learnmath/comments/3bi5kg/high_school_trigonometry_what_is_the_significance/
17. Unit Circle- Understanding Its Significance in Math - Gooroo Blog, accessed March 25, 2025, https://www.gooroo.com/blog/unit-circle/
18. Unit Circle: Sine and Cosine Functions | Precalculus - Lumen Learning, accessed March 25, 2025, https://courses.lumenlearning.com/precalculus/chapter/unit-circle-sine-and-cosine-functions/
19. The Unit Circle, accessed March 25, 2025, https://germanna.edu/sites/default/files/2022-03/Unit%20Circle.pdf
20. Unit Circle How to Find Coordinates on a Unit Circle (1) - YouTube, accessed March 25, 2025, https://www.youtube.com/watch?v=JMfGzvFTrR8
21. Master Coordinates in 7 MINUTES | Unit Circle - YouTube, accessed March 25, 2025, https://www.youtube.com/watch?v=UgE05IwjrJQ&pp=0gcJCfcAhR29_xXO
22. 7.3: Unit Circle - Math LibreTexts, accessed March 25, 2025, https://math.libretexts.org/Bookshelves/Algebra/Algebra_and_Trigonometry_1e_(OpenStax)/07%3A_The_Unit_Circle_-_Sine_and_Cosine_Functions/7.03%3A_Unit_Circle
23. demonstrations.wolfram.com, accessed March 25, 2025, https://demonstrations.wolfram.com/SineCosineTangentAndTheUnitCircle/#:~:text=The%20sine%20of%20the%20angle,same%20point%20and%20the%20origin.
24. 09 - Unit Circle - Definition & Meaning - Sin(x), Cos(x), Tan(x), - Sine, Cosine & Tangent, accessed March 25, 2025, https://www.youtube.com/watch?v=wCOtV44IUw4
25. Unit circle (video) | Trigonometry - Khan Academy, accessed March 25, 2025, https://www.khanacademy.org/math/algebra2/x2ec2f6f830c9fb89:trig/x2ec2f6f830c9fb89:unit-circle/v/unit-circle-definition-of-trig-functions-1
26. Sine, Cosine, Tangent and the Unit Circle - Wolfram Demonstrations Project, accessed March 25, 2025, https://demonstrations.wolfram.com/SineCosineTangentAndTheUnitCircle/
27. math.libretexts.org, accessed March 25, 2025, https://math.libretexts.org/Bookshelves/Precalculus/Precalculus_1e_(OpenStax)/05%3A_Trigonometric_Functions/5.02%3A_Unit_Circle_-_Sine_and_Cosine_Functions#:~:text=Using%20the%20unit%20circle%2C%20the,See%20Example.
28. Section 6.2: Trigonometric Functions: Unit Circle Approach | Precalculus Corequisite, accessed March 25, 2025, https://courses.lumenlearning.com/csn-precalculusv2/chapter/trigonometric-functions-unit-circle-approach/
29. Unit Circle Definition of Trig Functions - YouTube, accessed March 25, 2025, https://www.youtube.com/watch?v=ZffZvSH285c
30. The Unit Circle - Trigonometric Functions, accessed March 25, 2025, https://www.alamo.edu/contentassets/35e1aad11a064ee2ae161ba2ae3b2559/trigonometric/math2412-unit-circle.pdf
31. The Unit Circle: Your Guide to Understanding Trigonometry - SchoolTube, accessed March 25, 2025, https://www.schooltube.com/the-unit-circle-your-guide-to-understanding-trigonometry-2/
32. The Unit Circle: Your Guide to Understanding Trigonometry - SchoolTube, accessed March 25, 2025, https://www.schooltube.com/the-unit-circle-your-guide-to-understanding-trigonometry/
33. Trigonometric Graphs and the Unit Circle - YouTube, accessed March 25, 2025, https://www.youtube.com/watch?v=H0QveRy8OgY
34. 5.2: Unit Circle - Sine and Cosine Functions - Math LibreTexts, accessed March 25, 2025, https://math.libretexts.org/Bookshelves/Precalculus/Precalculus_1e_(OpenStax)/05%3A_Trigonometric_Functions/5.02%3A_Unit_Circle_-_Sine_and_Cosine_Functions
35. How do you find the point (x,y) on the unit circle that corresponds to the real number t=4π3?, accessed March 25, 2025, https://socratic.org/questions/how-do-you-find-the-point-x-y-on-the-unit-circle-that-corresponds-to-the-real-nu-4
36. How to Remember the Unit Circle (NancyPi) - YouTube, accessed March 25, 2025, https://www.youtube.com/watch?v=c819bGfH8FA
37. A Complete Guide to Deriving the Unit Circle from Scratch - YouTube, accessed March 25, 2025, https://www.youtube.com/watch?v=oyFEJPSWq9s
38. The Unit Circle | CK-12 Foundation, accessed March 25, 2025, https://flexbooks.ck12.org/cbook/ck-12-precalculus-concepts-2.0/section/5.1/primary/lesson/the-unit-circle-pcalc/
39. Explaining sine, cosine and tangent with the unit circle : r/interestingasfuck - Reddit, accessed March 25, 2025, https://www.reddit.com/r/interestingasfuck/comments/mh65k3/explaining_sine_cosine_and_tangent_with_the_unit/
40. Trig Visualized: One Diagram to Rule them All (six trig functions in one diagram) - YouTube, accessed March 25, 2025, https://www.youtube.com/watch?v=dUkCgTOOpQ0
41. Trigonometric Functions and the Unit Circle (Precalculus - Trigonometry 6) - YouTube, accessed March 25, 2025, https://www.youtube.com/watch?v=__nefjOhVks
42. Unit Circle With Tangent – Definition With Examples - Brighterly, accessed March 25, 2025, https://brighterly.com/math/unit-circle-with-tangent/
43. Solve Trig Equation with Unit Circle (4 examples) - YouTube, accessed March 25, 2025, https://www.youtube.com/watch?v=GCX7k3ildN0
44. 5-04 Solve Trigonometric Equations, accessed March 25, 2025, https://www.andrews.edu/~rwright/Precalculus-RLW/Text/05-04.html
45. 7.5 Solving Trigonometric Equations - Precalculus 2e | OpenStax, accessed March 25, 2025, https://openstax.org/books/precalculus-2e/pages/7-5-solving-trigonometric-equations
46. 3.6: Solving Trigonometric Equations - Mathematics LibreTexts, accessed March 25, 2025, https://math.libretexts.org/Courses/Las_Positas_College/Math_39%3A_Trigonometry/03%3A_Trigonometric_Identities_and_Equations/3.06%3A_Solving_Trigonometric_Equations
47. Solve trig equations with exact solutions - the easy way (unit circle) - YouTube, accessed March 25, 2025, https://m.youtube.com/watch?v=-ldZSvglx1A&t=439s
48. Solving Trig Equations: Using the Unit Circle - YouTube, accessed March 25, 2025, https://www.youtube.com/watch?v=Fo_cwq-Af1Y
49. Solve Trigonometric Equations Using the Unit Circle - Expii, accessed March 25, 2025, https://www.expii.com/t/solve-trigonometric-equations-using-the-unit-circle-5259
50. Solve trig equations with exact solutions - the easy way (unit circle) - YouTube, accessed March 25, 2025, https://www.youtube.com/watch?v=-ldZSvglx1A
51. brainly.com, accessed March 25, 2025, https://brainly.com/question/31591129#:~:text=Periodicity%20of%20Sine%20and%20Cosine%3A&text=This%20means%20that%20these%20functions,and%20cosine%20functions%20are%20periodic.
52. Prove that Sine and Cosine are Periodic Functions - YouTube, accessed March 25, 2025, https://www.youtube.com/watch?v=H0WfsmmYjqs
53. Sine and Cosine Periodicity Identities - YouTube, accessed March 25, 2025, https://www.youtube.com/watch?v=iFkpwvNTksI
54. Periods of sine, cosine and tangent - Trigonometry Facts: The Amazing Unit Circle, accessed March 25, 2025, https://mathmistakes.info/facts/TrigFacts/learn/uc/per.html
55. unacademy.com, accessed March 25, 2025, https://unacademy.com/content/ssc/study-material/mathematics/differences-between-radian-and-degree/#:~:text=One%20degree%20is%20equivalent%20to%200.017453%20radians%2C%20and%201%20radian,degree%20by%20180%C2%B0%2F%20%CF%80.
56. Learn what is a radian and degree and the difference between them, accessed March 25, 2025, https://unacademy.com/content/ssc/study-material/mathematics/differences-between-radian-and-degree/
57. Radians & degrees (video) | Trigonometry - Khan Academy, accessed March 25, 2025, https://www.khanacademy.org/math/algebra2/x2ec2f6f830c9fb89:trig/x2ec2f6f830c9fb89:radians/v/radian-and-degree-conversion-practice
58. MFG The Unit Circle, accessed March 25, 2025, https://mathbooks.unl.edu/PreCalculus/unit-circle.html
59. Intuitive Guide to Angles, Degrees and Radians - BetterExplained, accessed March 25, 2025, https://betterexplained.com/articles/intuitive-guide-to-angles-degrees-and-radians/
60. Radians and Degrees - YouTube, accessed March 25, 2025, https://www.youtube.com/watch?v=JmLN3QxshlE
61. flexbooks.ck12.org, accessed March 25, 2025, https://flexbooks.ck12.org/cbook/ck-12-algebra-ii-with-trigonometry-concepts/section/13.6/primary/lesson/introduction-to-the-unit-circle-and-radian-measure-alg-ii/#:~:text=In%20other%20words%20the%20arc,multiply%20by%20180%20%E2%88%98%20%CF%80%20.
62. Relation Between Degree and Radian | Conversion and Examples - BYJU'S, accessed March 25, 2025, https://byjus.com/maths/relation-between-degree-and-radian/
63. Unit circle trigonometry | Lesson (article) - Khan Academy, accessed March 25, 2025, https://www.khanacademy.org/test-prep/v2-sat-math/x0fcc98a58ba3bea7:geometry-and-trigonometry-easier/x0fcc98a58ba3bea7:unit-circle-trigonometry-easier/a/v2-sat-lesson-unit-circle-trigonometry
64. Introduction to the Unit Circle and Radian Measure | CK-12 Foundation, accessed March 25, 2025, https://flexbooks.ck12.org/cbook/ck-12-algebra-ii-with-trigonometry-concepts/section/13.6/primary/lesson/introduction-to-the-unit-circle-and-radian-measure-alg-ii/
65. [Precalculus] Struggling with the idea of Radians and the unit circle : r/learnmath - Reddit, accessed March 25, 2025, https://www.reddit.com/r/learnmath/comments/2a7r3n/precalculus_struggling_with_the_idea_of_radians/