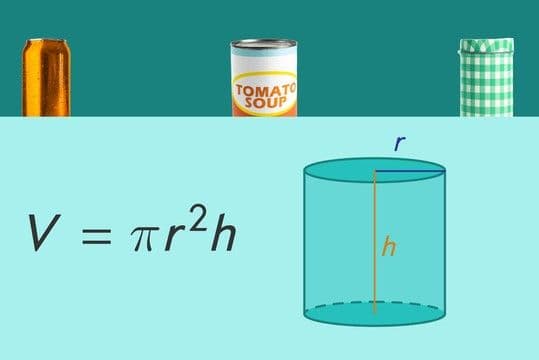Introduction
The volume of a cylinder is a fundamental concept in geometry, representing the amount of space inside the cylinder. It is calculated using the formula V=πr²h, where r is the radius of the circular base and h is the height of the cylinder. This formula is essential for understanding various real-world applications, from engineering and manufacturing to everyday uses like storing water or fuel.
Understanding the volume of a cylinder is not just about memorizing a formula; it involves grasping the underlying principles of geometry and applying them to solve real-world problems. In this post, we'll delve into the basics of the formula, explore its practical applications, discuss tips for accurate calculations, address common challenges, and look at future trends in the field.

Practical Insights and Benefits
Understanding the Formula
The formula for the volume of a cylinder, V=πr²h, is derived by multiplying the area of the circular base (πr²) by the height (h) of the cylinder. This simple yet powerful formula is the foundation for calculating volumes in a wide range of applications.
Practical Application
This formula helps in calculating the capacity of cylindrical containers, such as water tanks or fuel tanks, ensuring efficient storage and usage. For instance, if you're planning to install a water tank in your backyard, knowing the volume will help you determine how much water it can hold, which is crucial for planning water supply during emergencies or for irrigation purposes.
Real-World Applications
The volume of a cylinder has numerous practical applications across various industries:
- Engineering and Manufacturing: Calculating the volume of cylinders is crucial for designing and producing cylindrical components like pipes and tanks. Engineers use this formula to ensure that structures are strong enough to hold the required amount of material without collapsing under pressure.
- Food and Beverage Industry: Determining the volume of cans and bottles ensures proper packaging and storage. This is important for maintaining product quality and preventing waste during transportation and storage.
- Construction: Calculating the volume of cylindrical structures like pillars and columns is vital for material estimation and structural integrity. Builders need to ensure that these structures can support the weight of the building without compromising safety.

In-Depth Analysis
Derivation of the Formula
The volume of a cylinder can be visualized as a stack of circular disks. Each disk has an area of πr², and when stacked to a height h, the total volume is the product of the area and height, resulting in πr²h, and when stacked to a height . This conceptual understanding helps in applying the formula to different scenarios.
Mathematical Insights
The formula V=πr²h is a direct application of the principle that the volume of a solid can be found by integrating the area of its cross-sections over its height. In the case of a cylinder, since the cross-sectional area remains constant, the integration simplifies to multiplication.
Geometric Properties
Cylinders have several geometric properties that make them useful in various applications:
- Symmetry: Cylinders are symmetric about their axis, which makes them stable and balanced.
- Curved Surface Area: The curved surface area of a cylinder is given by 2πrh, which is important for calculating the surface area that needs to be covered or coated.

Tips and Strategies
Calculating Volume with Diameter
If the diameter (d) is known instead of the radius, use r=d⁄2 in the formula to find the volume. This is particularly useful when measurements are given in terms of diameter, which is common in engineering and construction.
Avoiding Common Mistakes
- Incorrect Units: Ensure all measurements are in the same units (e.g., meters or centimeters) to avoid calculation errors. Mixing units can lead to incorrect results.
- Rounding Too Early: Carry exact values through calculations to maintain accuracy. Rounding prematurely can introduce significant errors, especially in precise applications.
Using Approximations
In some cases, approximating π as 3.14 is sufficient for rough estimates. However, for precise calculations, using a more accurate value of π (e.g., 3.14159) is recommended.

Common Challenges and Solutions
Distorted Shapes
For distorted cylinders, approximating the shape as a regular cylinder or using more complex mathematical models can help estimate the volume. This might involve breaking down the shape into simpler components or using numerical methods to approximate the volume.
Limited Measurements
If only the diameter and height are known, use r=d⁄2 to calculate the volume. This is a straightforward solution but requires careful attention to unit conversions.
Non-Uniform Cross-Sections
In cases where the cylinder does not have a uniform cross-section (e.g., tapered cylinders), the volume calculation becomes more complex. It may involve integrating the varying cross-sectional areas over the height or using specialized formulas for specific shapes.
Future Outlook and Trends
Advanced Materials and Designs
Future trends may involve using advanced materials to create lighter yet stronger cylindrical structures, enhancing efficiency in various industries. For example, using carbon fiber or advanced polymers could reduce the weight of cylinders while maintaining their strength, which is particularly beneficial in aerospace and automotive applications.
Sustainability
Calculating the volume of cylinders will become increasingly important in sustainable practices, such as optimizing storage and reducing waste in industries like manufacturing and construction. Efficient use of materials and space can significantly reduce environmental impact by minimizing the need for additional resources and reducing waste.
Technological Advancements
Advancements in technology, such as 3D printing and computer-aided design (CAD), will continue to play a crucial role in designing and optimizing cylindrical structures. These tools allow for precise modeling and simulation, enabling engineers to test and refine designs before physical production.

Conclusion
Understanding the volume of a cylinder is more than just applying a formula; it involves grasping the underlying geometric principles and applying them to solve real-world problems. From engineering and manufacturing to everyday applications, the volume of a cylinder plays a vital role in ensuring efficiency, safety, and sustainability.